
38 39の問題教えて頂きたいです お願いします Clearnote
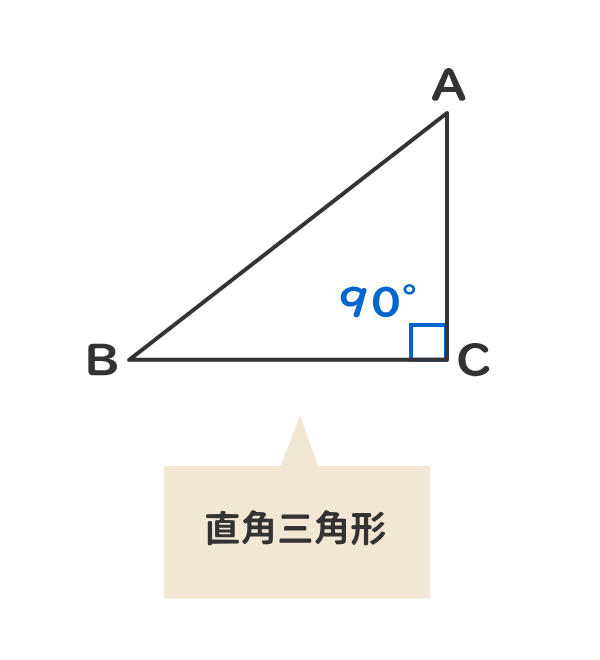
直角三角形 (ちょっかくさんかくけい、 英 right triangle )は、 三角形 の一種である。 三角形の3つの内角のうち、他のどの内角よりも小さくない角に注目したとき、その角が 直角 (90 ° =π/2 rad) に等しい 図形 を指す。 直角三角形 直角三角形の各 辺 の長さの関係は ピタゴラスの定理 (三平方の定理)と呼ばれる。 記号 ⊿ を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直★三平方の定理 〜「2つの特別な直角三角形 」〜 小学校から使ってきた「2つの三角定規」は、実は"特別"だった! 特に、「正三角形の1辺の長さから高さが求まる」は、いつでも思いつくよう
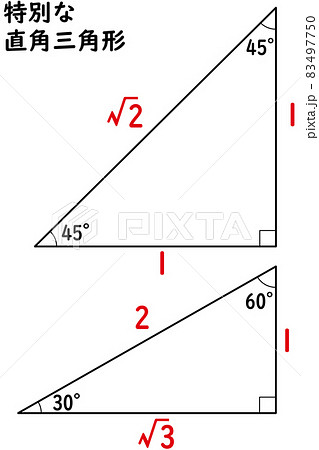
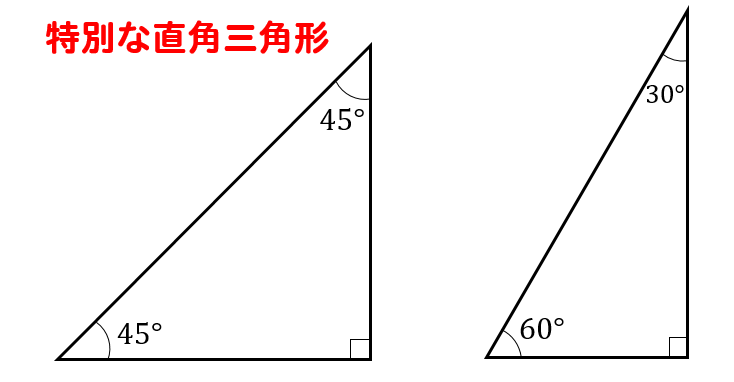
特別 な 直角 三角形
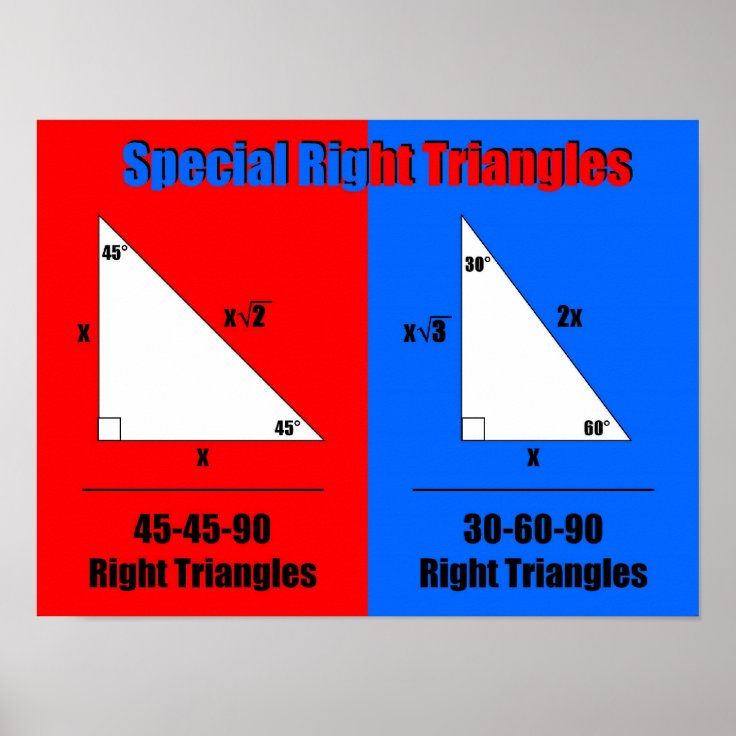
特別 な 直角 三角形-特殊直角三角形を解く方法は? 特殊直角三角形、または30 6090三角形を解くための公式は単純です。 短脚、長脚、斜辺を知っていれば、すべての測定値を簡単に見つけることができます。 短い脚の長さaがわかっている場合は、次のことがわかります。 b 右側が少々太くなっているので、それは「デルタ」(微少な変化)では? 確かに直角三角形という意味で「⊿」のような記号を用いることもできますが、 ふつうテストなんかでは使いません。 「すうがく」で変換可能です。

特別な直角三角形の辺の比 無料で使える中学学習プリント
三平方の定理 座標平面の特別な直角三角形 図の直線lは y= 3 4 x のグラフで, 点P,Qはともに直線lのグラフ上の点である。 点Aの座標が (8,0)で, PQAが正三角形のとき線分PQの長さを求めよ。 P Q O A (8, 0) x y l B (8,6) 点Aから直線lにおろした垂線の長さを求める。 直線l上のx=8の点をBとする。 図の直線lはy=7x, 点P,Qはともに直線l上にある。 線分PAの長さを求めよ。 A (2,0) x y O今回は、 「直角三角形の合同」 について学習するよ。 三角形の合同条件の3つのパターンは、もうマスターしているかな? 実は、直角三角形の場合は、それに加えて、 特別な2つの合同条件 というものが存在するよ。 それが、今日のポイント。さらに特別な角の三角比の確認 ★特別な角の三角比からさらに特別な角の三角比を求めよう。 60 や135 など特別な角の三角比の値はよく用いますね。 これらの特別な角以外に、一般的な図形から求められる三角比の値はないでしょうか?
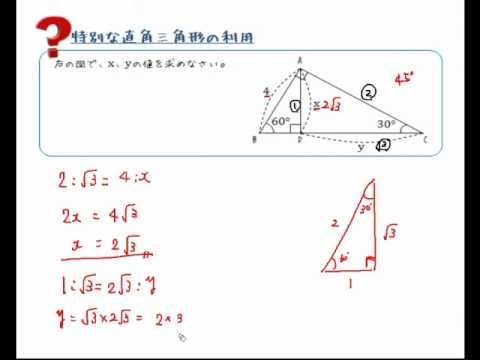
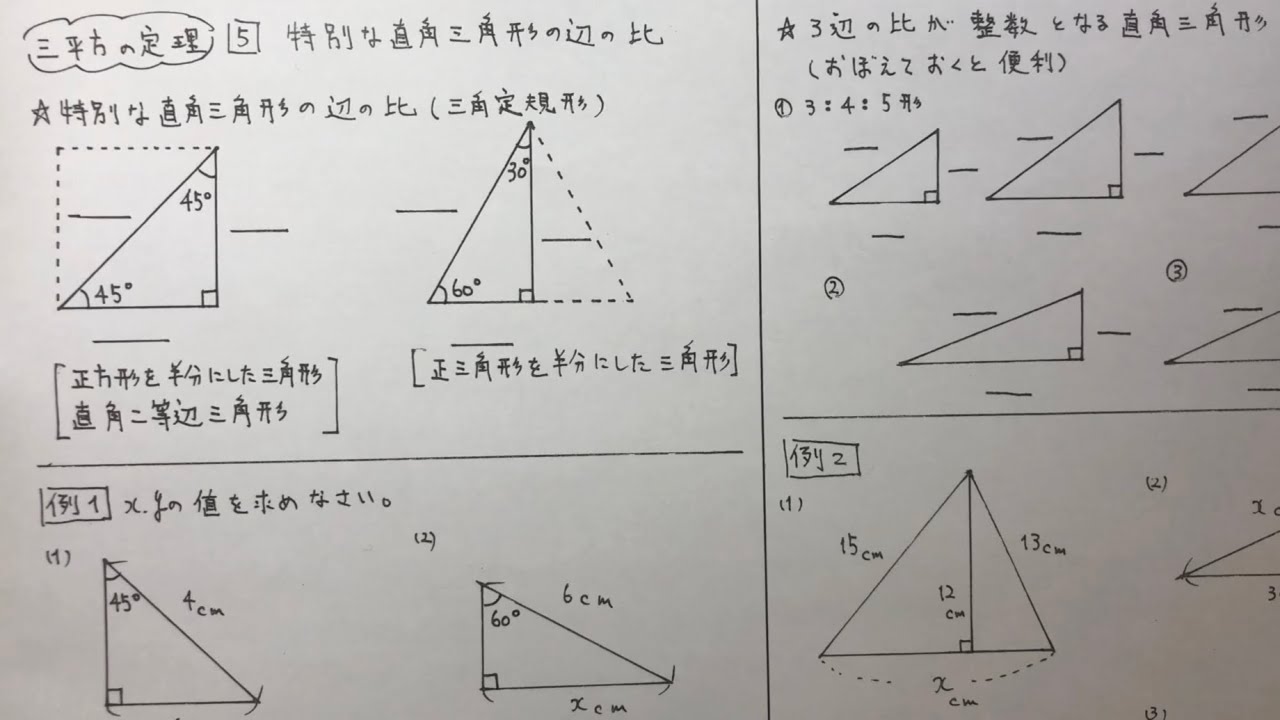
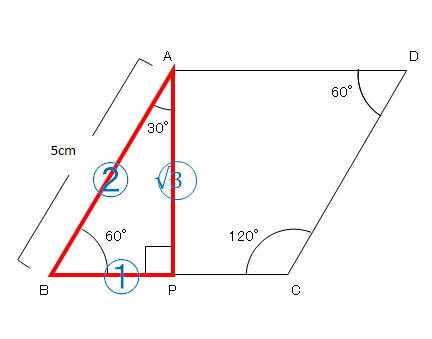
特別な直角三角形2 例題1xの値を求める。 1° 12 4 x a b c aからbcの延長上に垂線をおろして交点をdとする。 acdは60°, 30°, 90°の三角形となるので accdad = 21 3 である。 accd = 21 12cd = 21 cd = 6 acad = 2 3 12ad = 2 3 ad= 6 3 1° 4 x a b c 12 d 60° 直角三角 中3 三平方の定理 カテゴリーの記事一覧 すべて無料! 星組の中学数学講座 授業動画は声と手だけ、テキストは下手な字で手書きの低クオリティー! だけど、内容は役に立つと思います。 また、無料学習プリント集としてもお使いいただけます ホーム 中学数学 図形 直角三角形とは? 定義や定理、辺の長さの比、合同条件 21年12月17日 この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひ
特別 な 直角 三角形のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
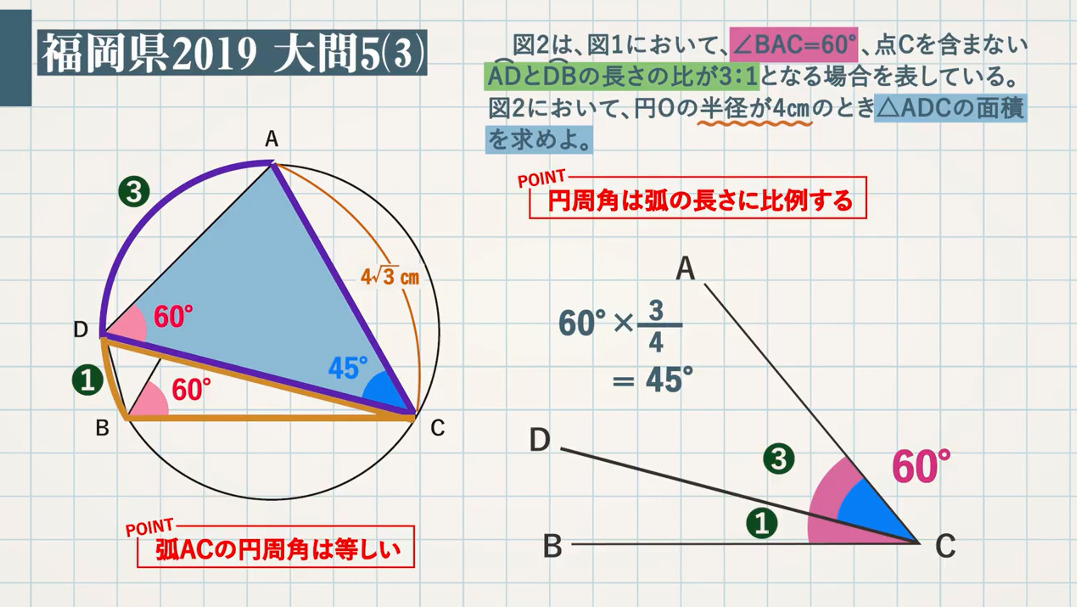 |  | 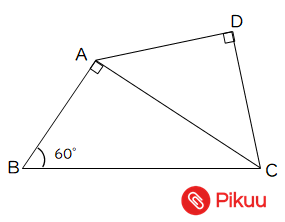 |
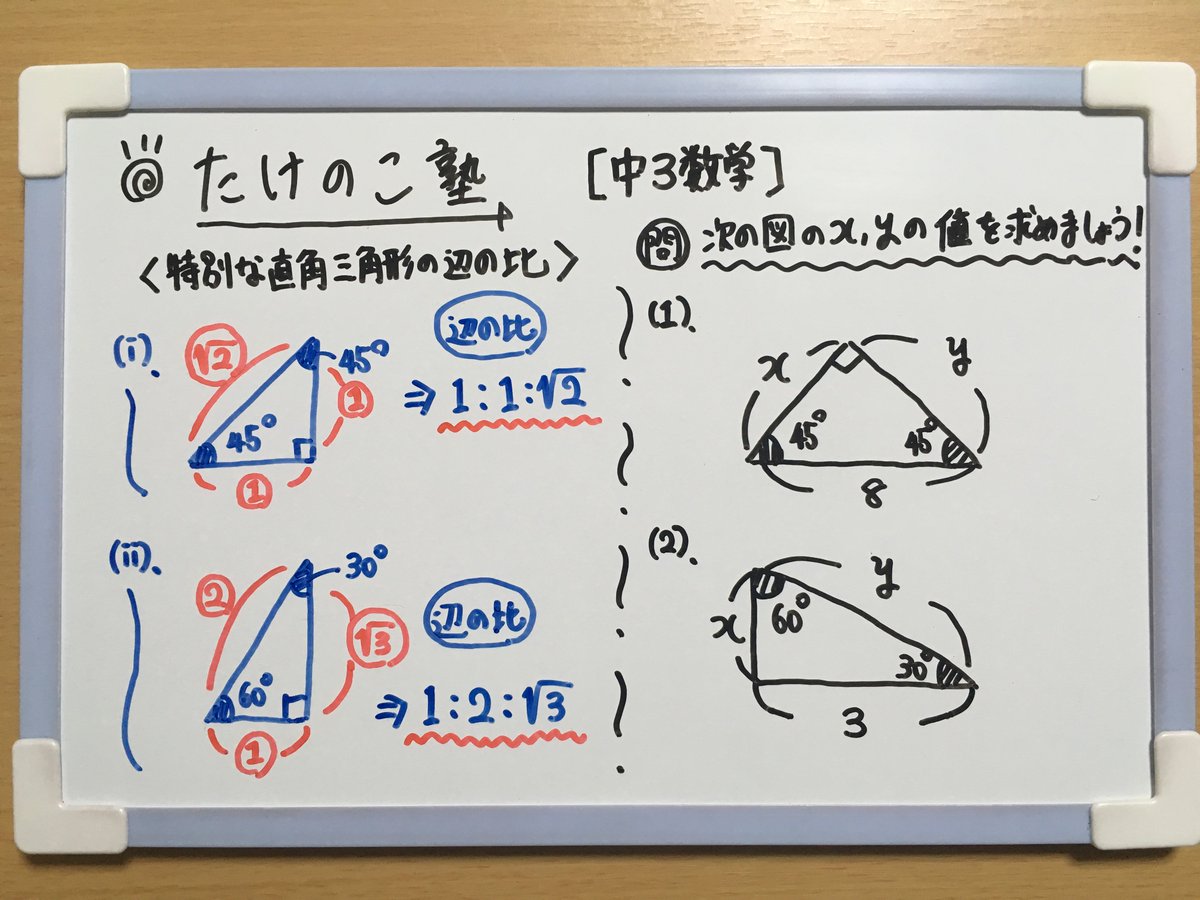 |  |  |
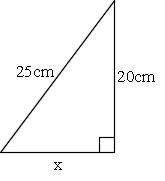 |  | |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「特別 な 直角 三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
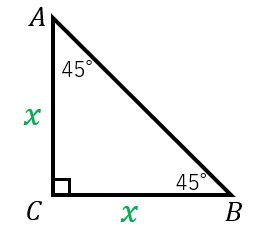 |  |  |
 |
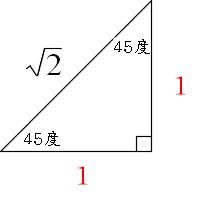
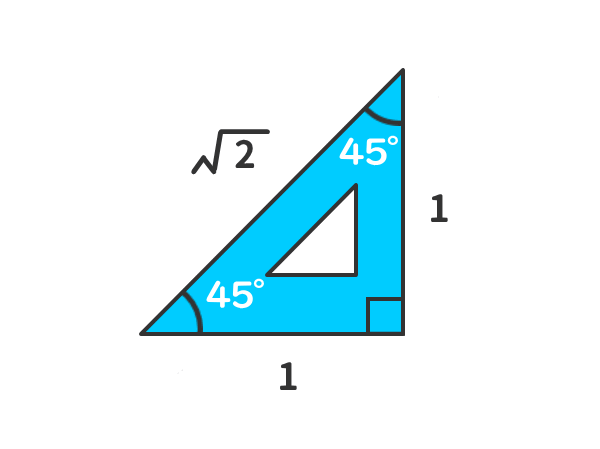
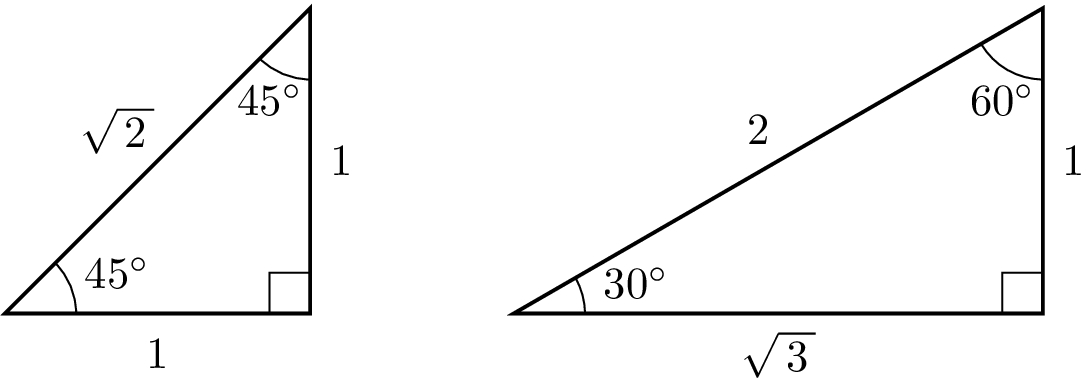
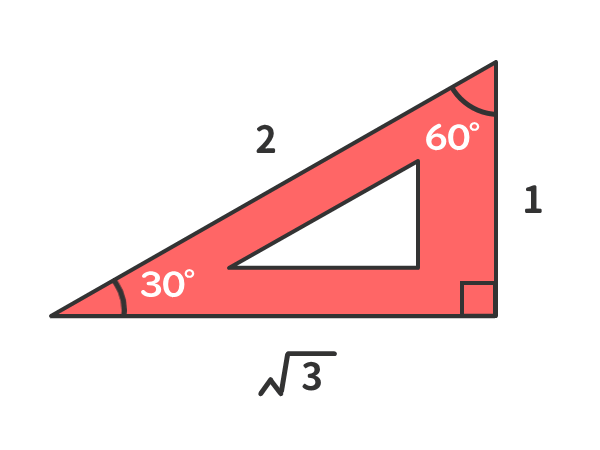
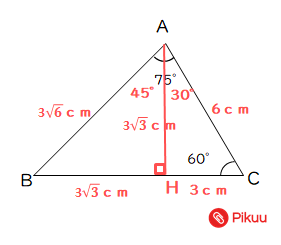
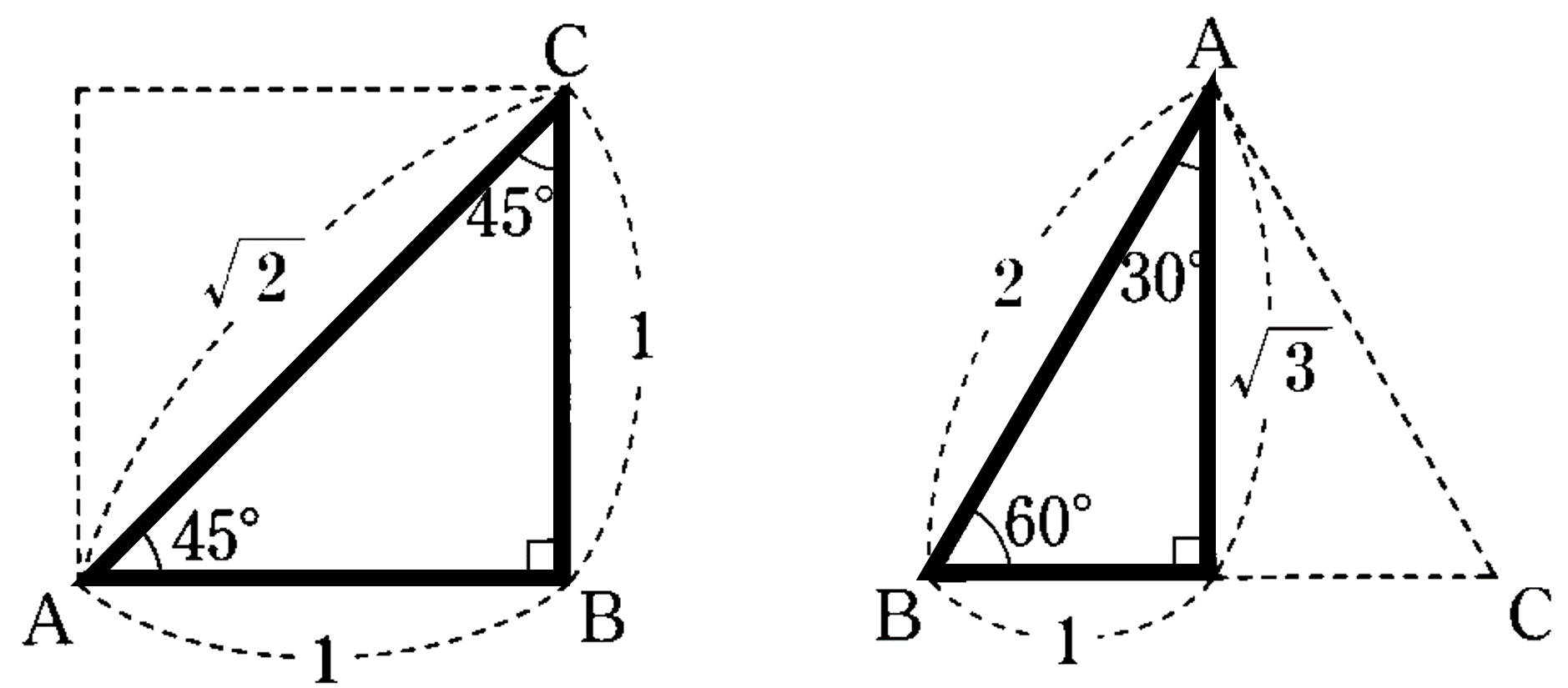
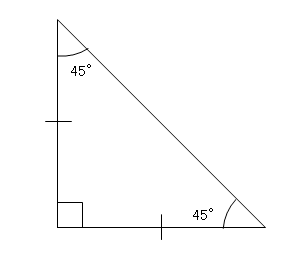
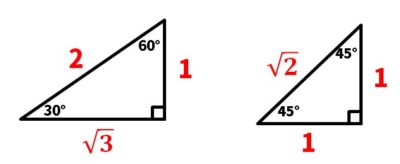
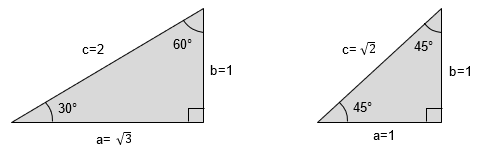
暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角二等辺三角特別な直角三角形 特別な直角三角形 解説 ABCの面積を求めよ。 105° 30° 6cm A B C ABCの面積を求めよ。 A B C 6cm 15° 15° 図の ABCについて答えよ。 2cm 75° 75° A B C 辺ABの長さを求めよ。 ABCの面積を求めよ。 pdfファイル 解説表示 三平方の定理 要点 三平方の定理 三平方の定理 平面での利用 特別な直角三角形 三平方の定理 立体での利用 三平方の定理 例題





0 件のコメント:
コメントを投稿